Все выпуски

Дополнительные материалы:

Видеоролики компьютерных экспериментов представлены в виде GIF-анимаций (Визуализации 1-16). GIF-анимации запускаются и перезапускаются автоматически. Чтобы остановить визуализацию на определенной итерации, нужно загрузить анимацию и открыть ее в видеоплеере, например в Media Player Classic.

Визуализация 1. Модель 1 с окрестностью Мура.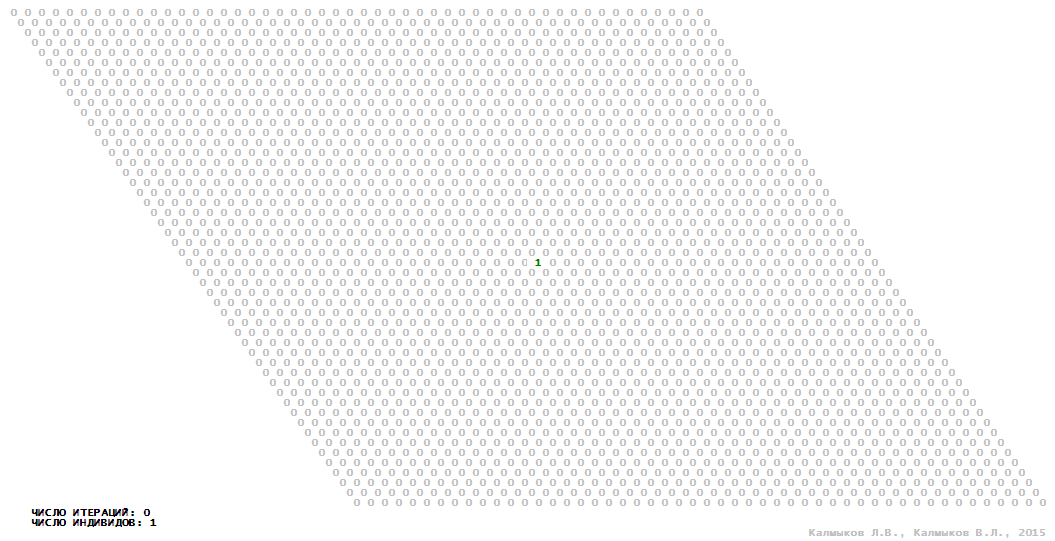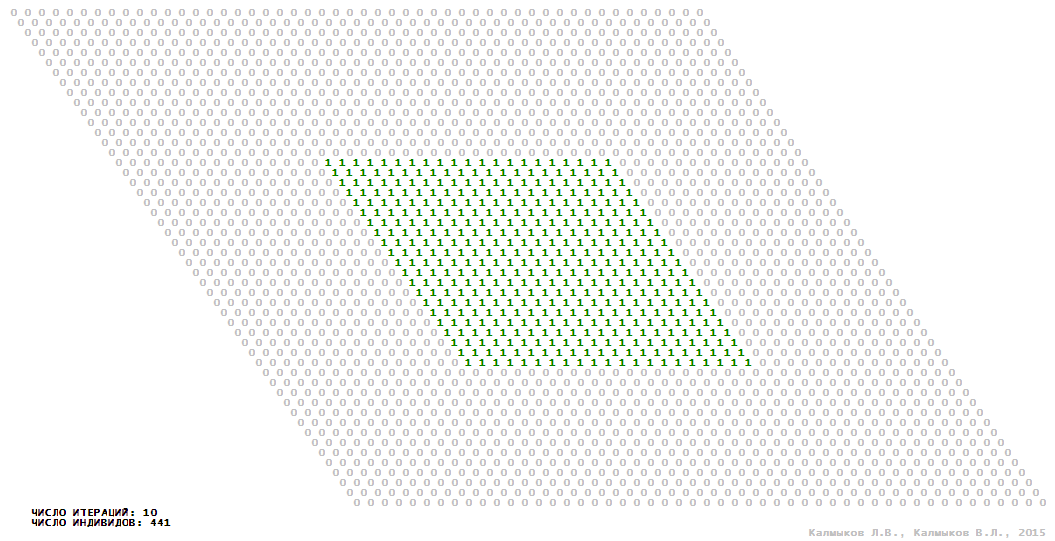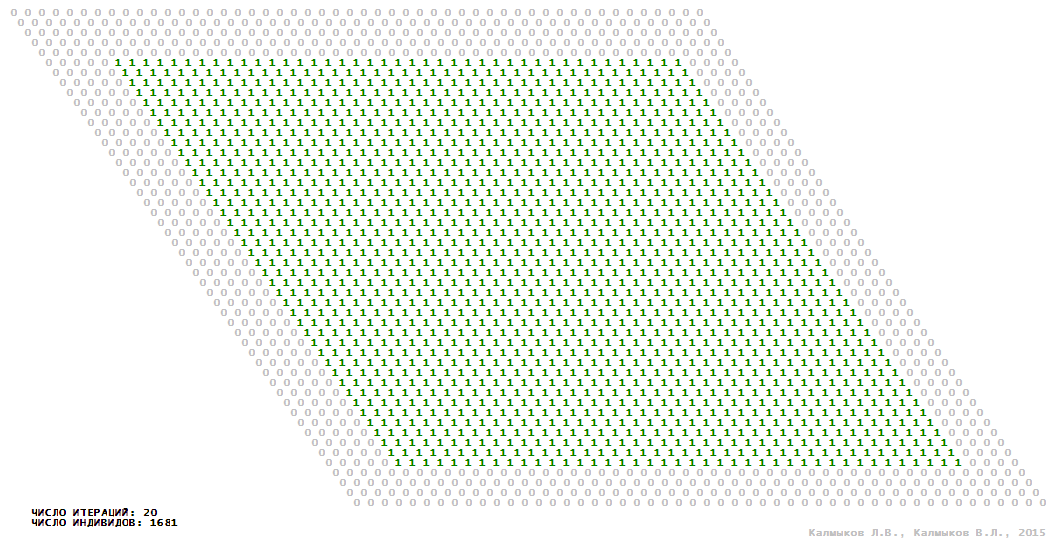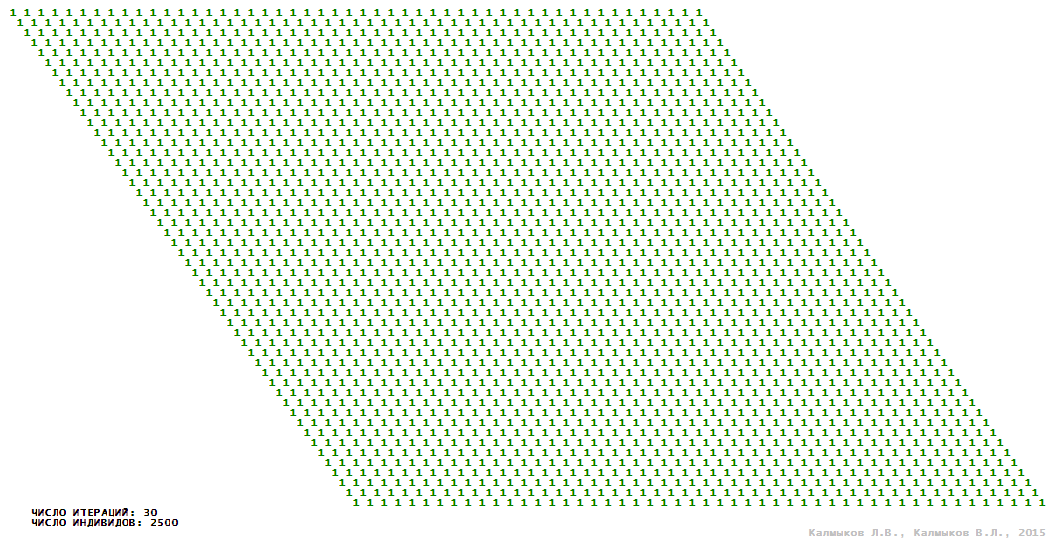

Визуализация 2. Модель 1 с гексагональной окрестностью.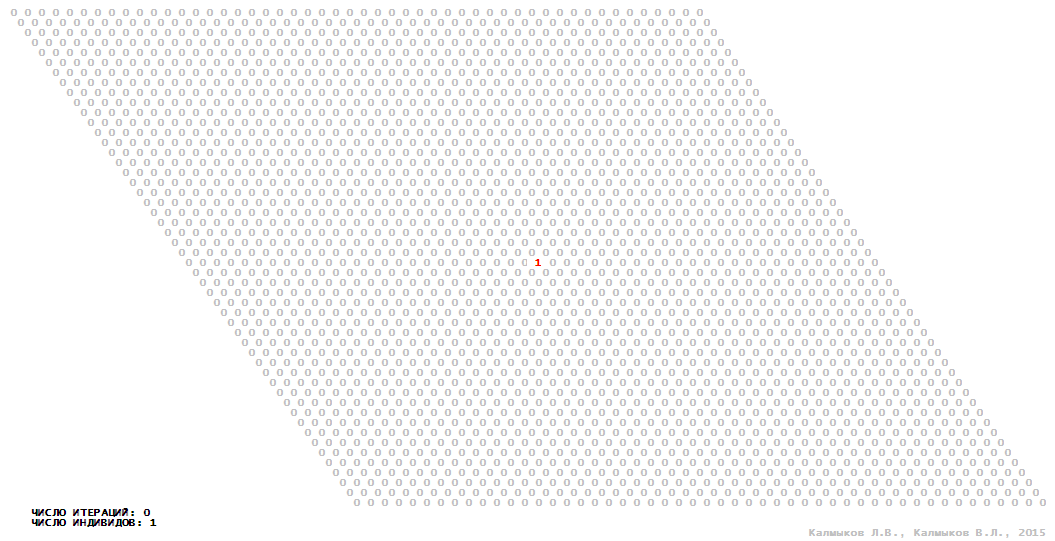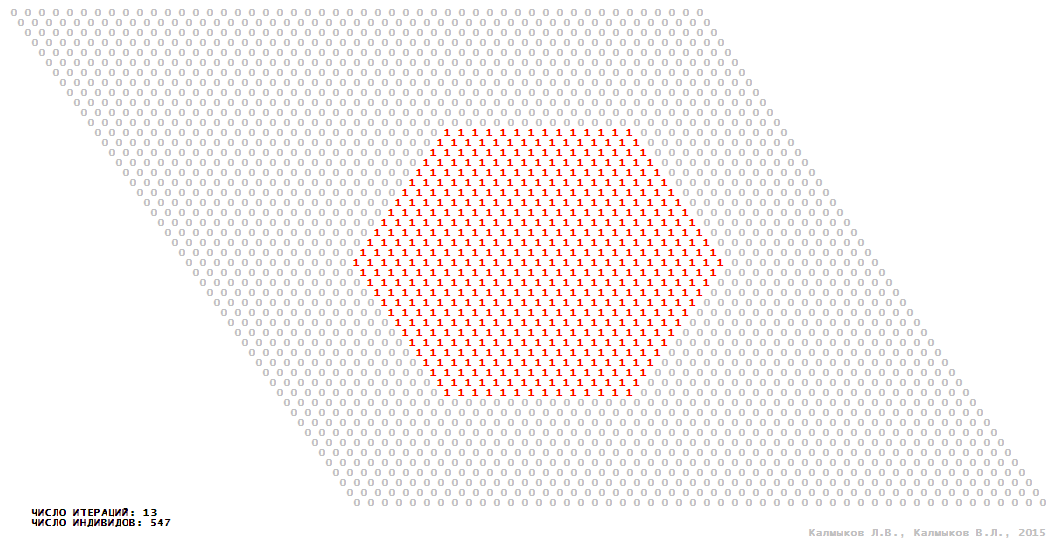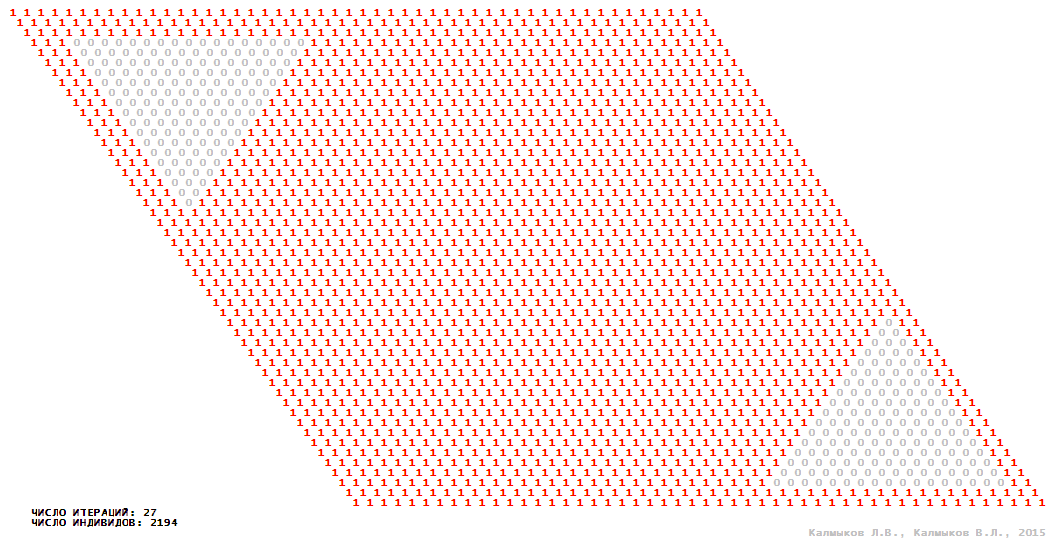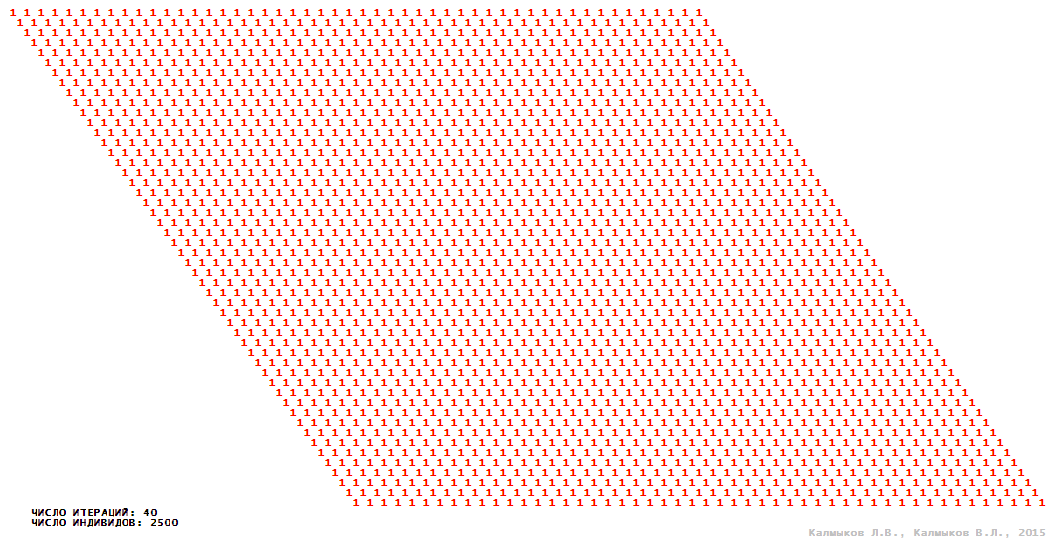

Визуализация 3. Модель 1 с окрестностью фон Неймана.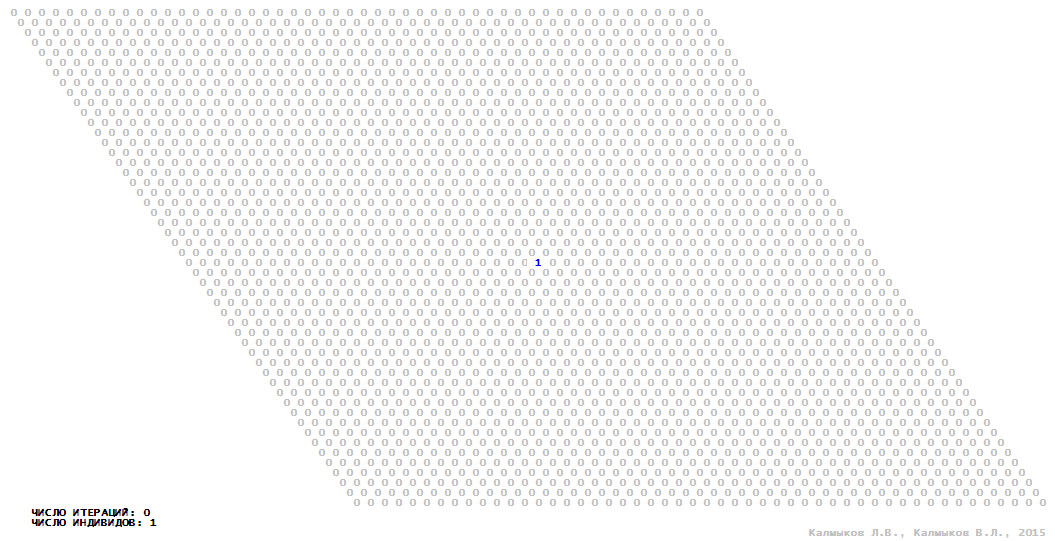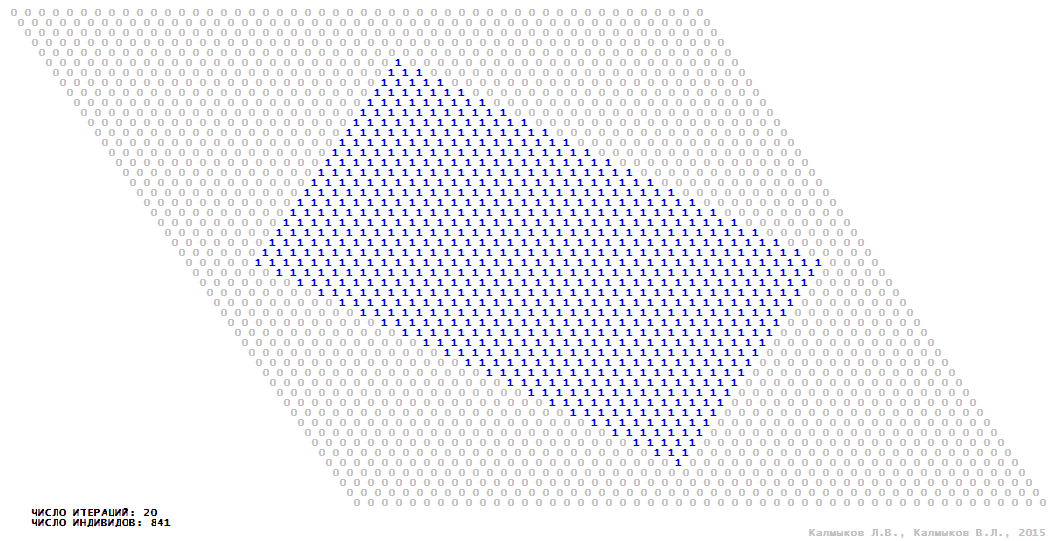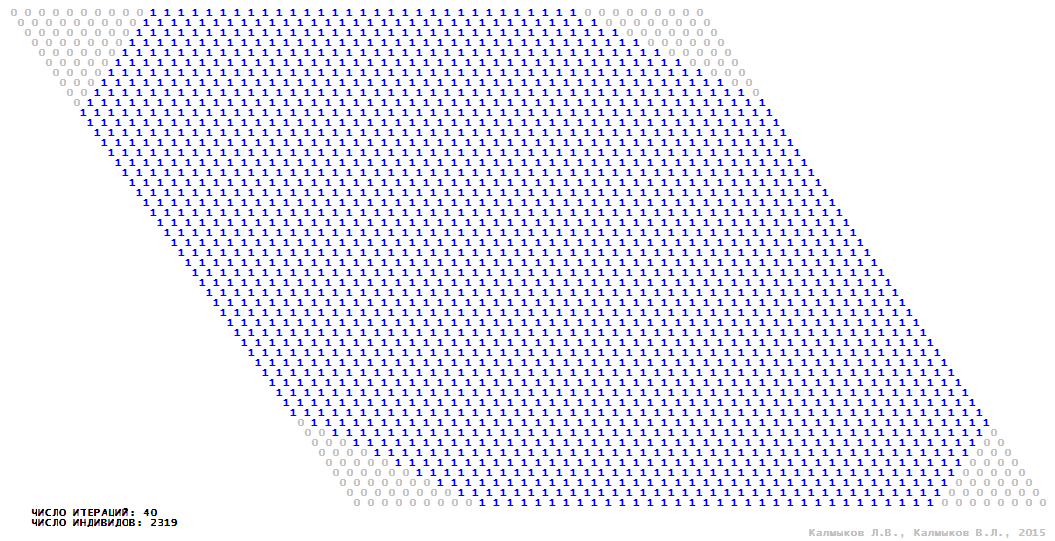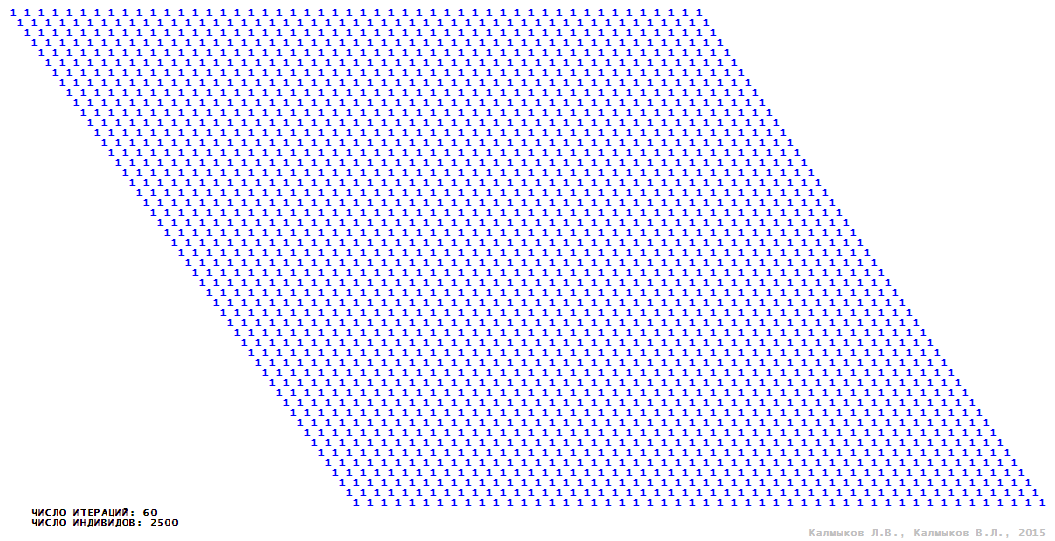

Визуализация 4. Модель 1 с триподной окрестностью.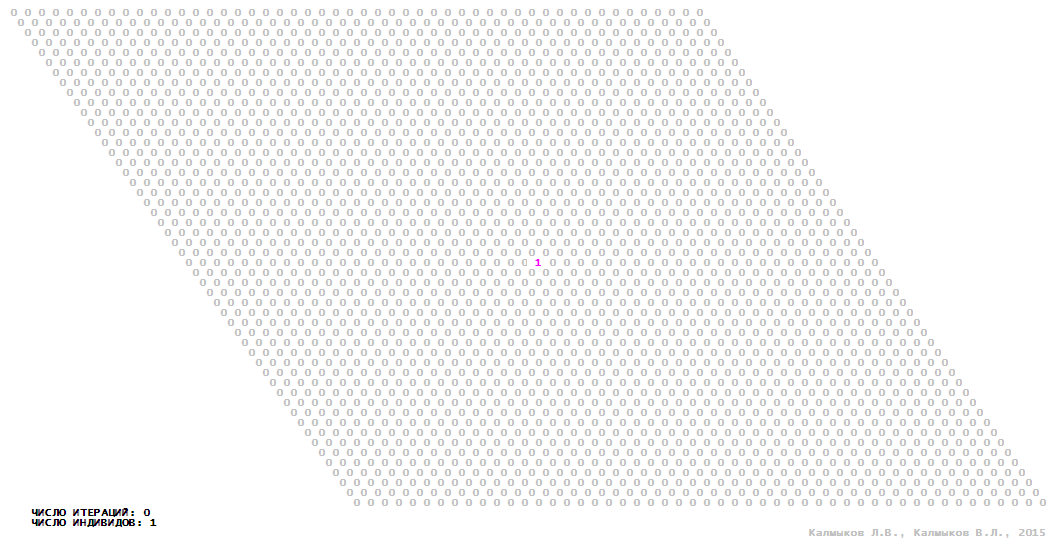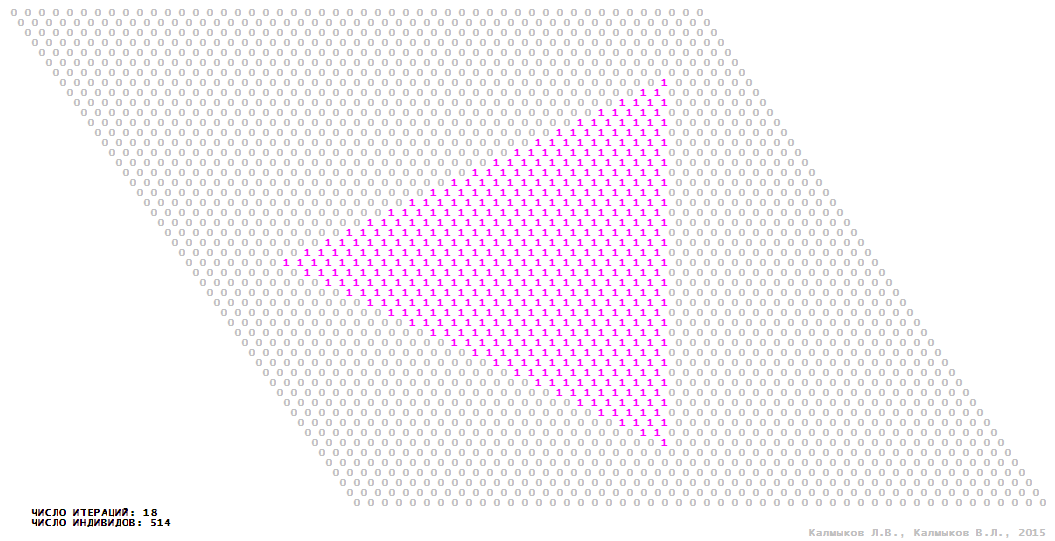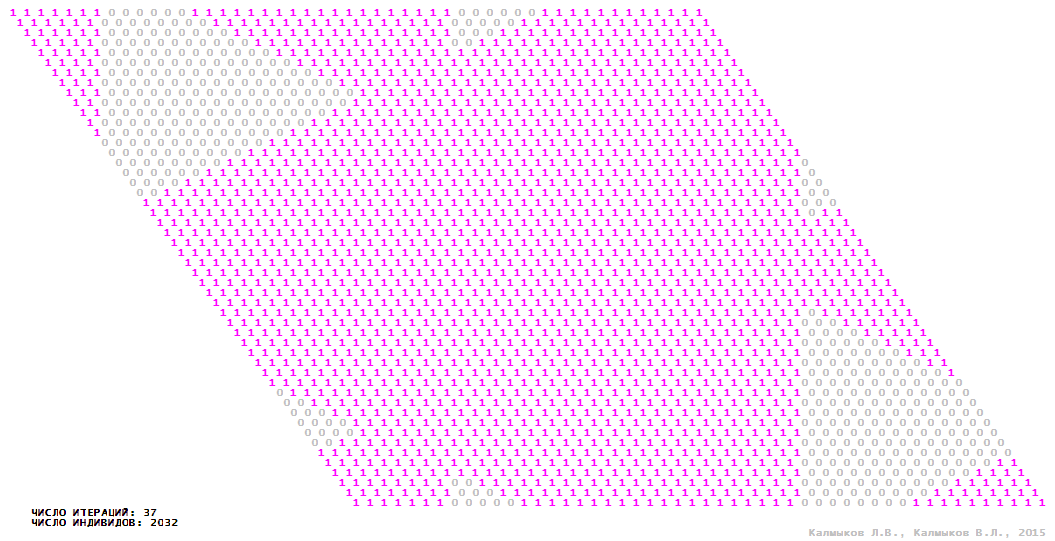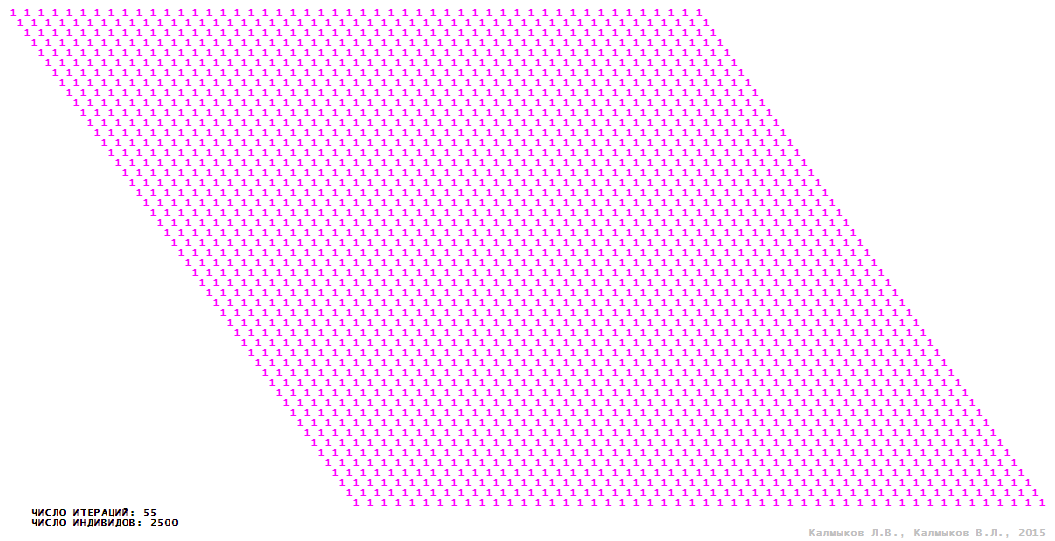

Модель 1 — логический детерминированный клеточный автомат с двумя состояниями. Множество возможных состояний каждого узла решётки {0, 1}. Решётка клеточного автомата состоит из 50x50 узлов и замкнута периодическими условиями в тор. Регенерация ресурсов и утилизация отмершей особи происходит одновременно с жизнедеятельностью вновь заселённого индивида. Используются обозначения: {0} — микроместообитание свободно; {1} — микроместообитание заселено индивидом. С помощью различных окрестностей исследуется влияние числа потомков и их размещение в пространстве на популяционную динамику. Кривые популяционного роста имеют S-образную форму и представлены на Рисунке 10а. Во всех четырёх случаях происходила успешная колонизация свободного местообитания, и далее вид продолжал существовать неограниченно долго.

Визуализация 5. Модель 2 с окрестностью Мура.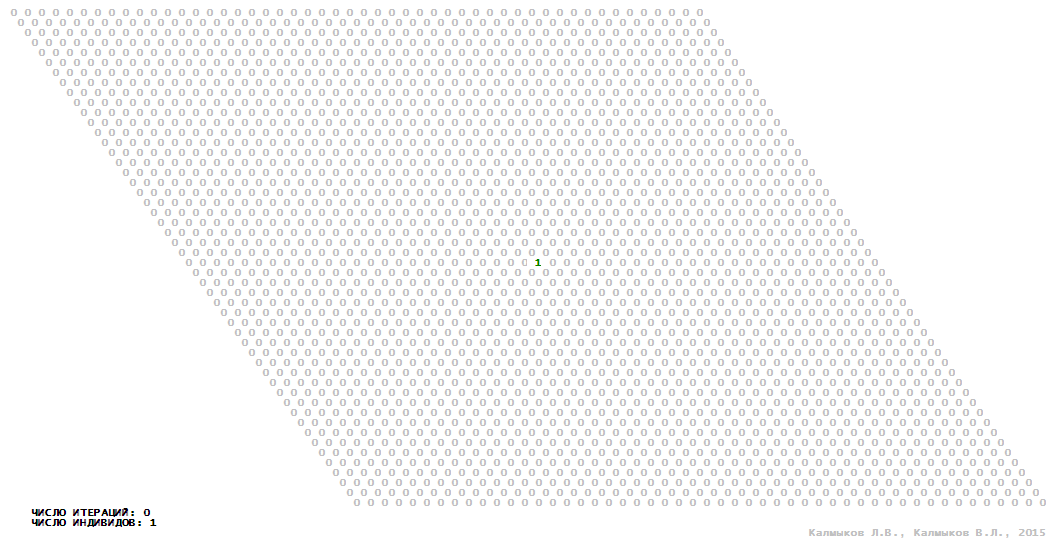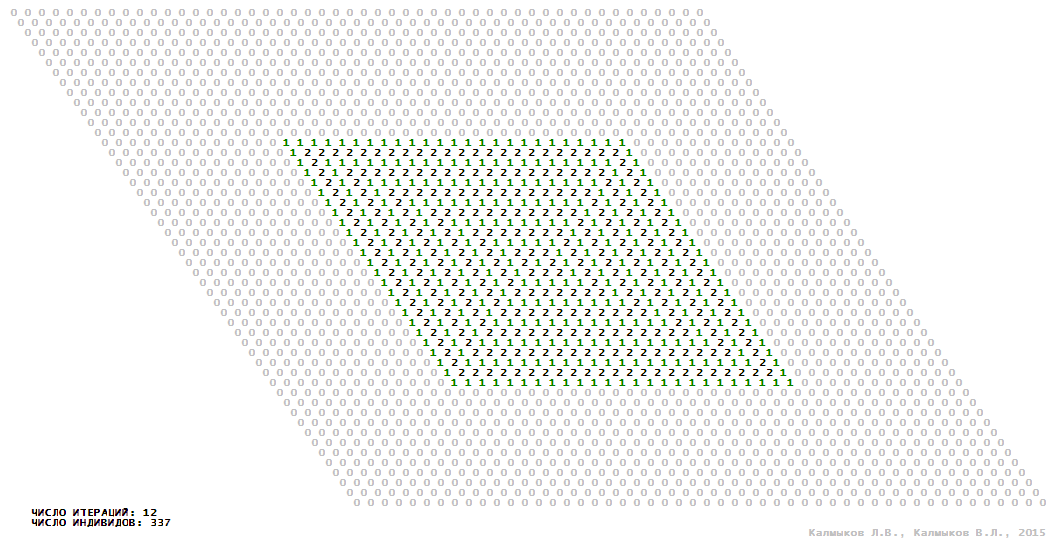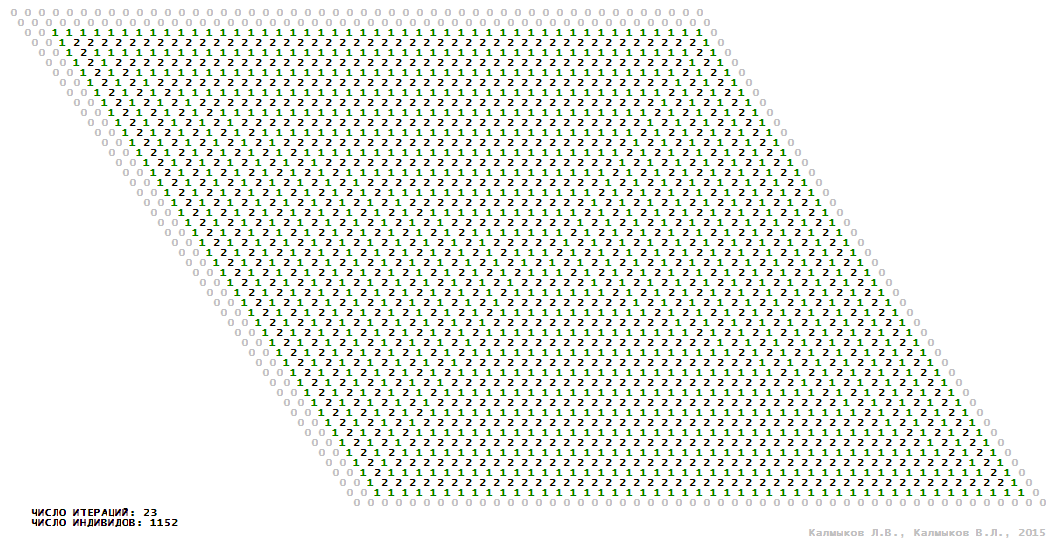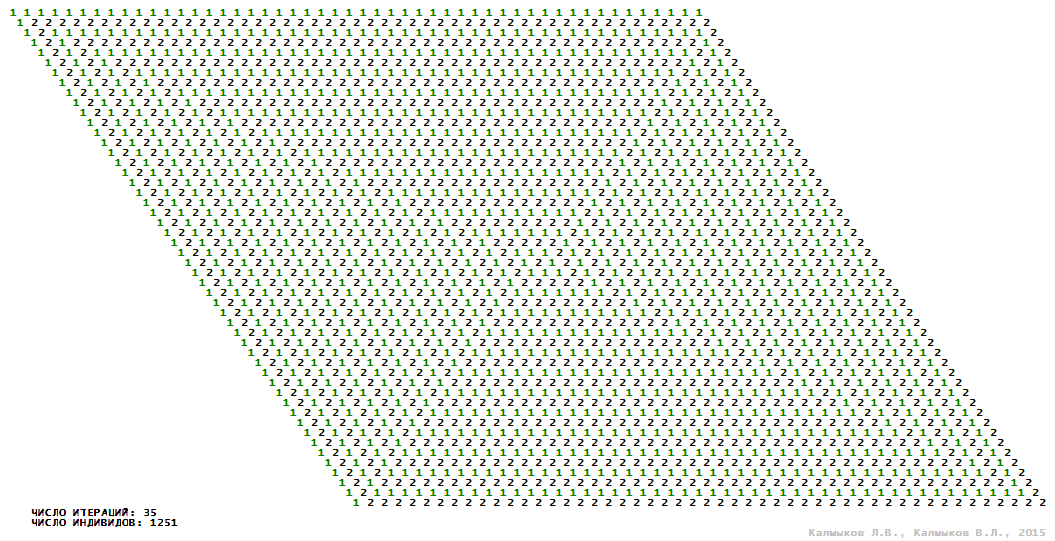

Визуализация 6. Модель 2 с гексагональной окрестностью.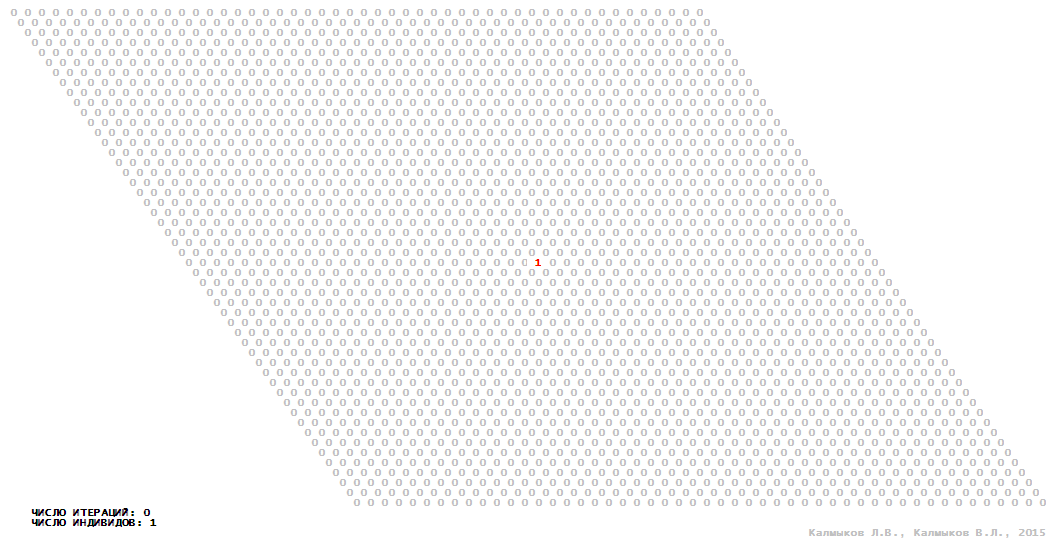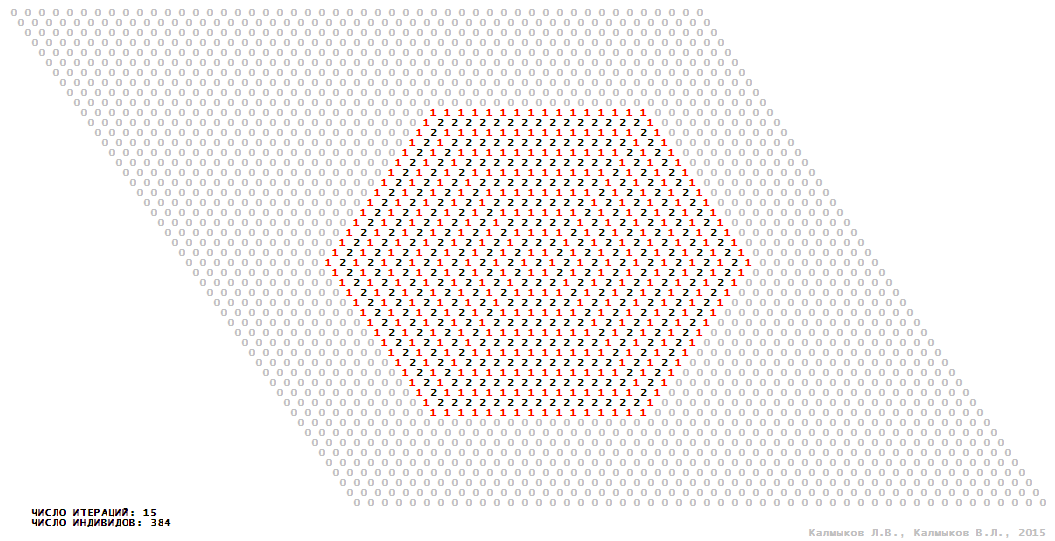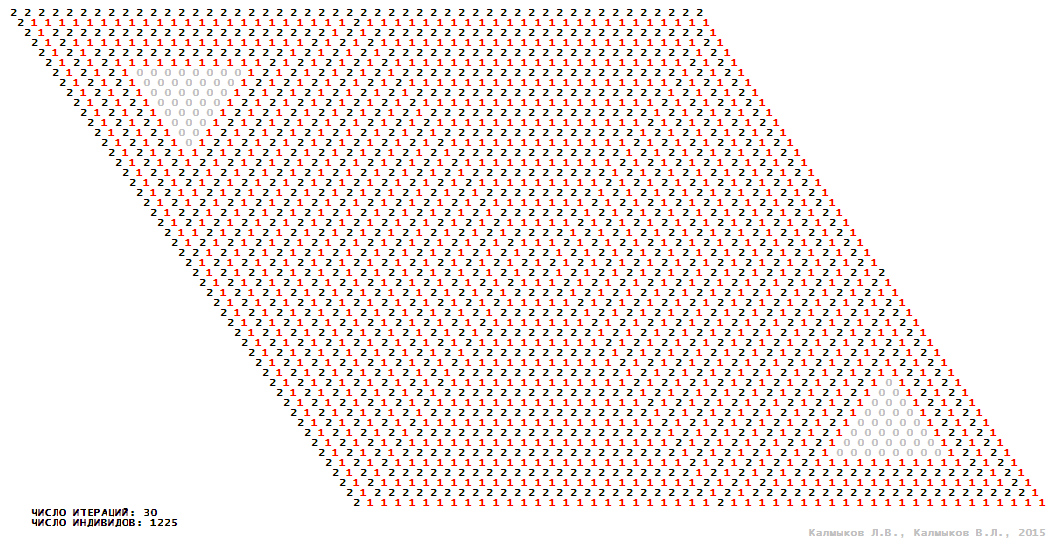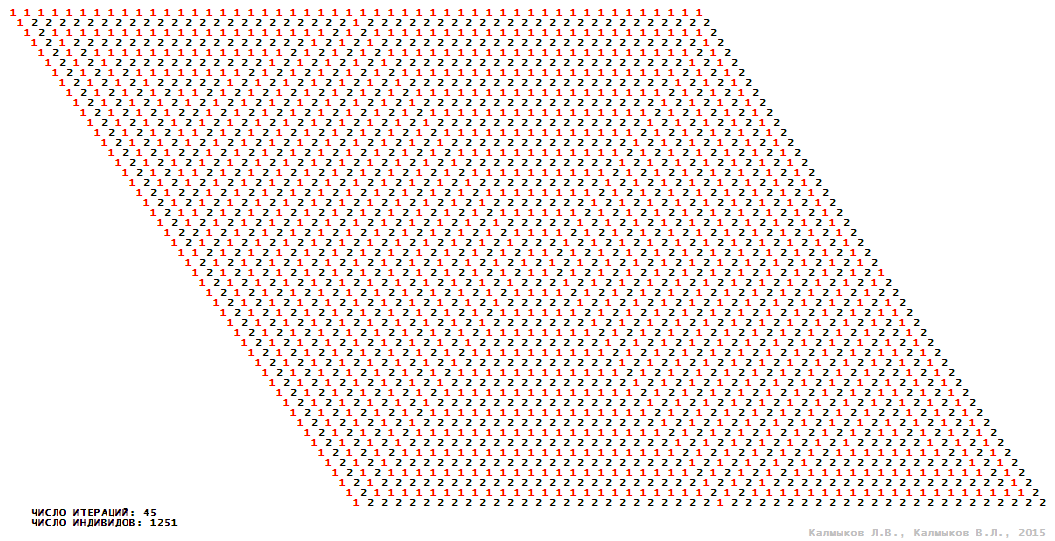

Визуализация 7. Модель 2 с окрестностью фон Неймана.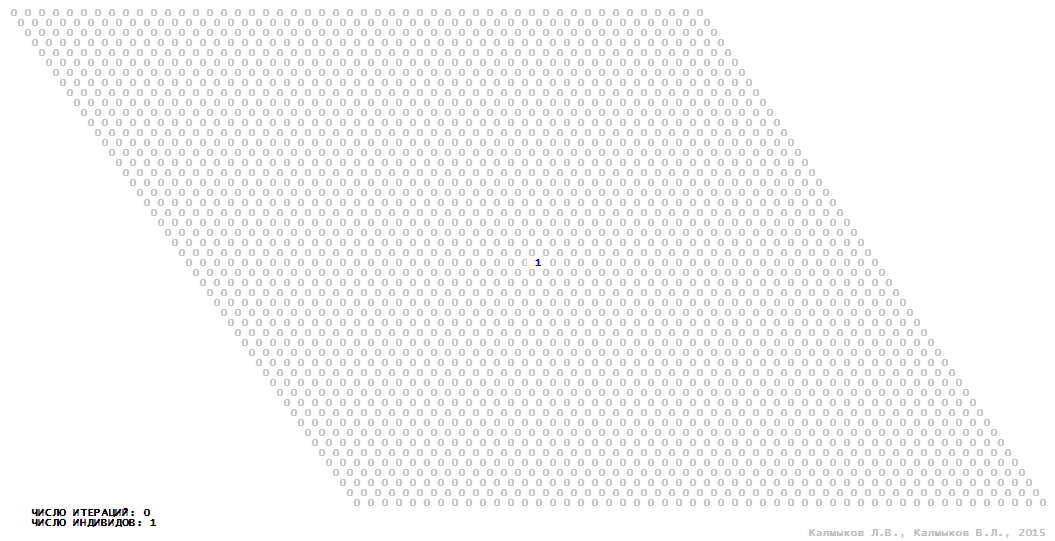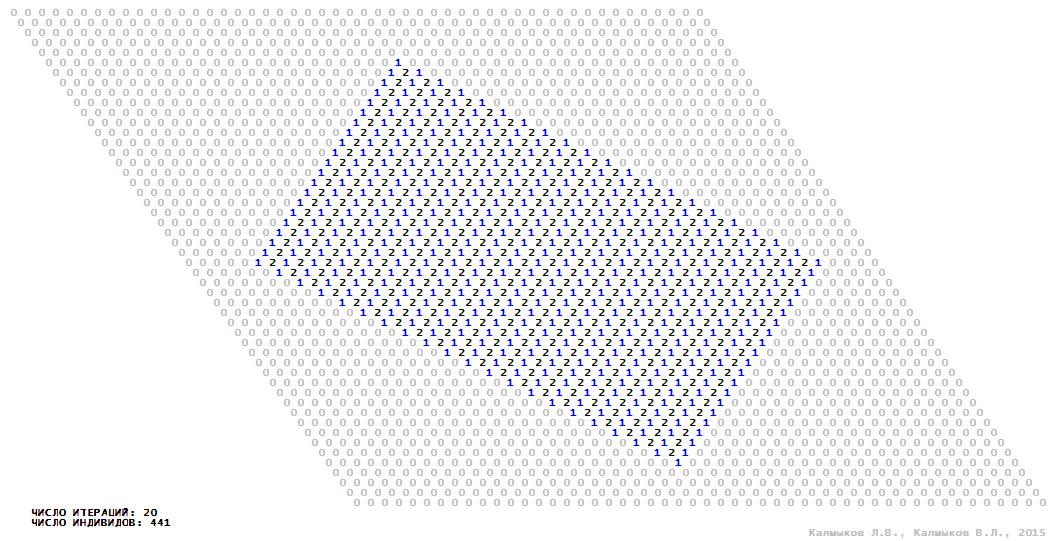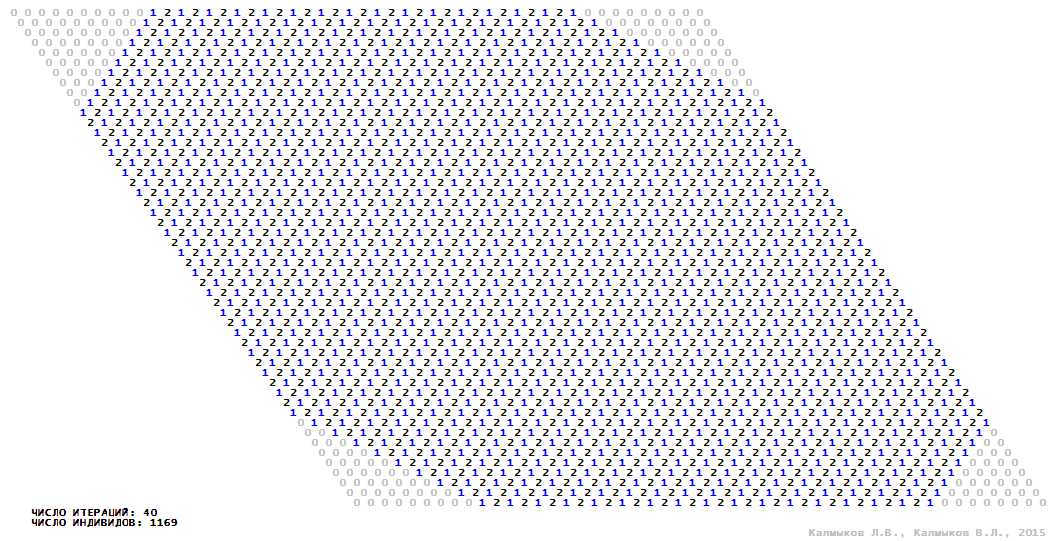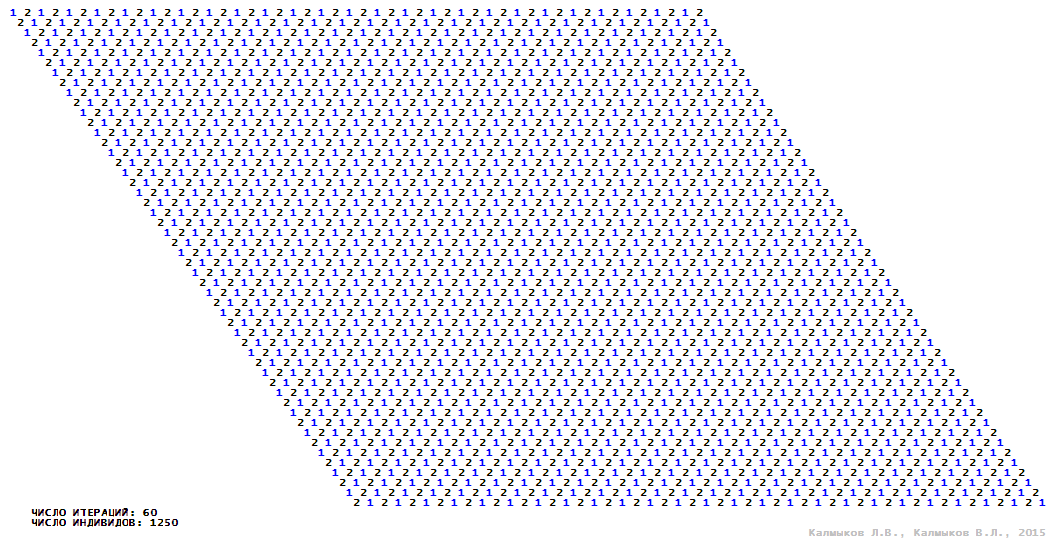

Визуализация 8. Модель 2 с триподной окрестностью.

Модель 2 — логический детерминированный клеточный автомат с тремя состояниями. Множество возможных состояний каждого узла решётки {0, 1, 2}. Решётка клеточного автомата состоит из 50x50 узлов и замкнута периодическими условиями в тор. Длительность восстановления ресурсов занимает одну итерацию. Используются обозначения: {0} — микроместообитание свободно; {1} — микроместообитание заселено индивидом; {2} — микроместообитание находится в состоянии регенерации, которое длится одну итерацию. С помощью различных окрестностей исследуется влияние числа потомков и их размещение в пространстве на популяционную динамику. При использовании окрестностей Мура, гексагональной и фон Неймана кривые популяционного роста имеют S-образную форму (Рис. 10б). При использовании триподной окрестности кривая популяционного роста имеет двойную S-образную форму (Рис. 10б). Во всех четырёх случаях происходила успешная колонизация свободного местообитания, и далее вид продолжал существовать неограниченно долго.

Визуализация 9. Модель 3 с окрестностью Мура.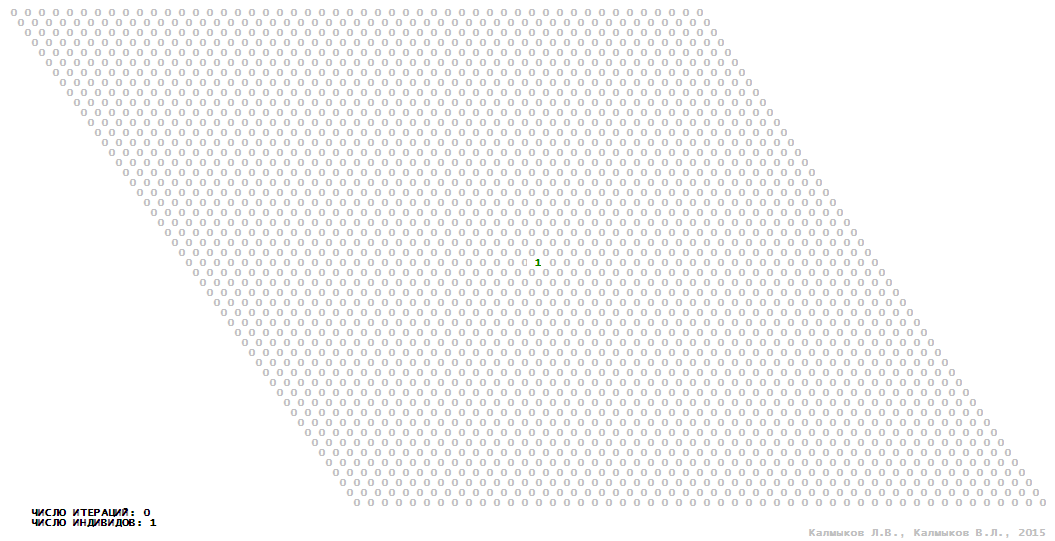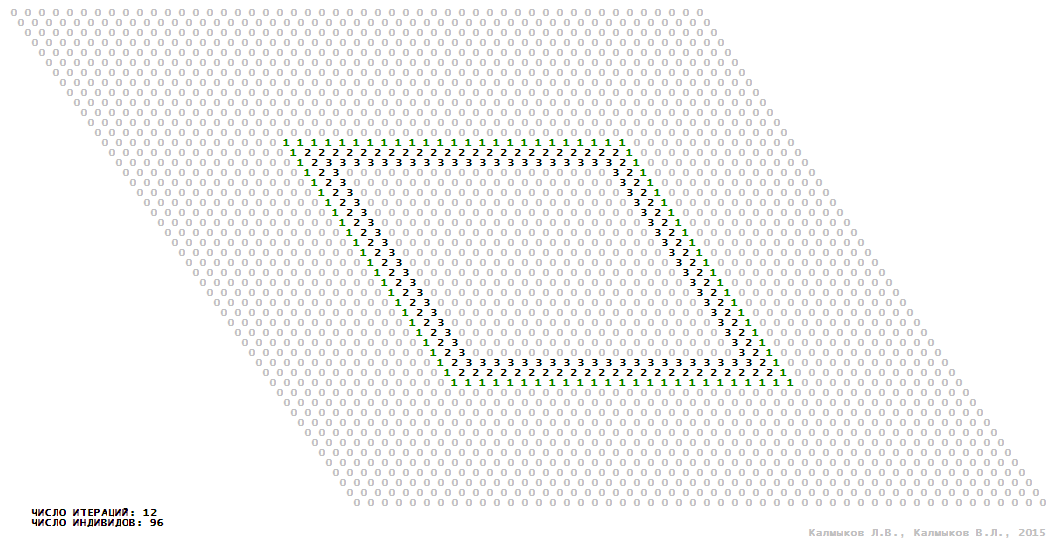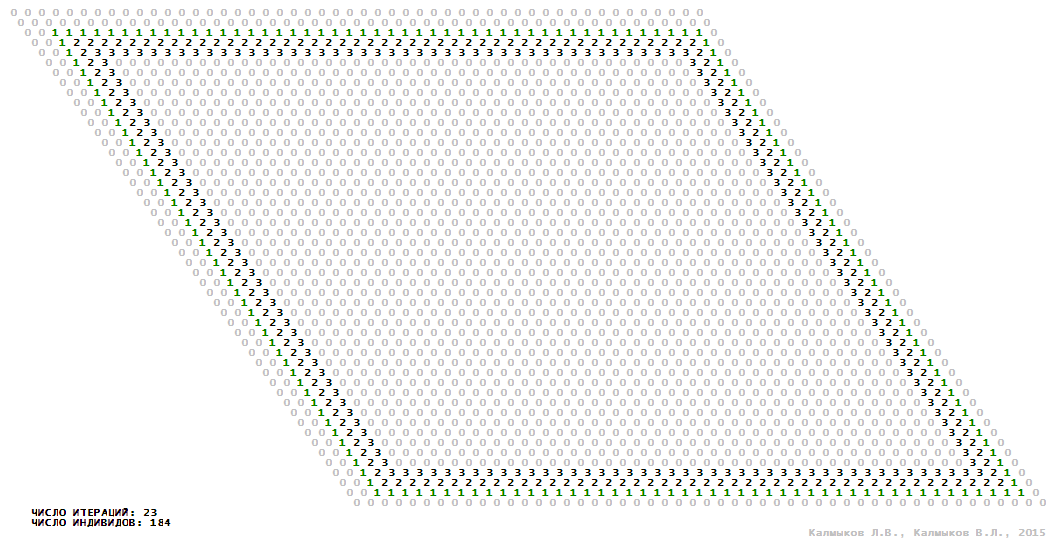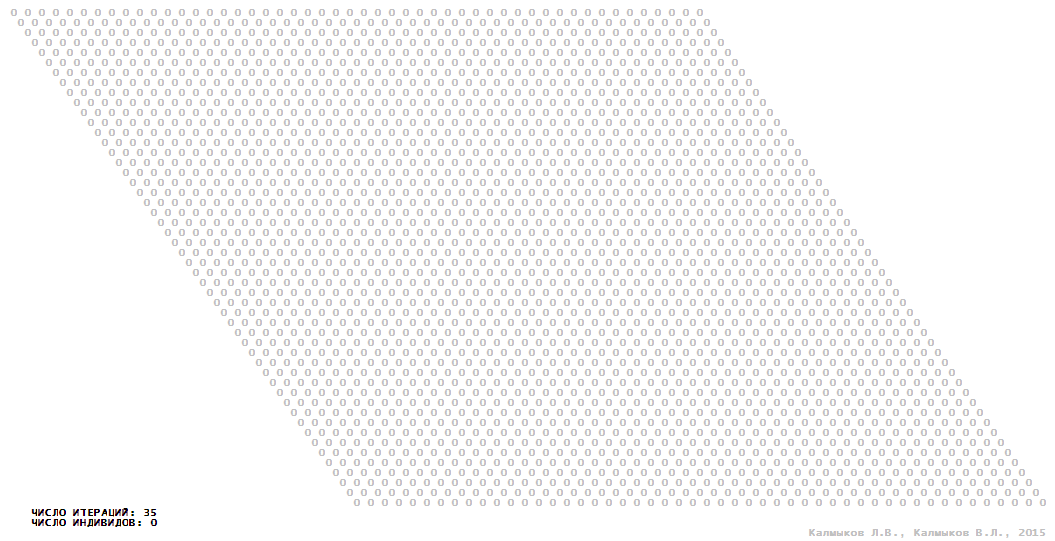

Визуализация 10. Модель 3 с гексагональной окрестностью.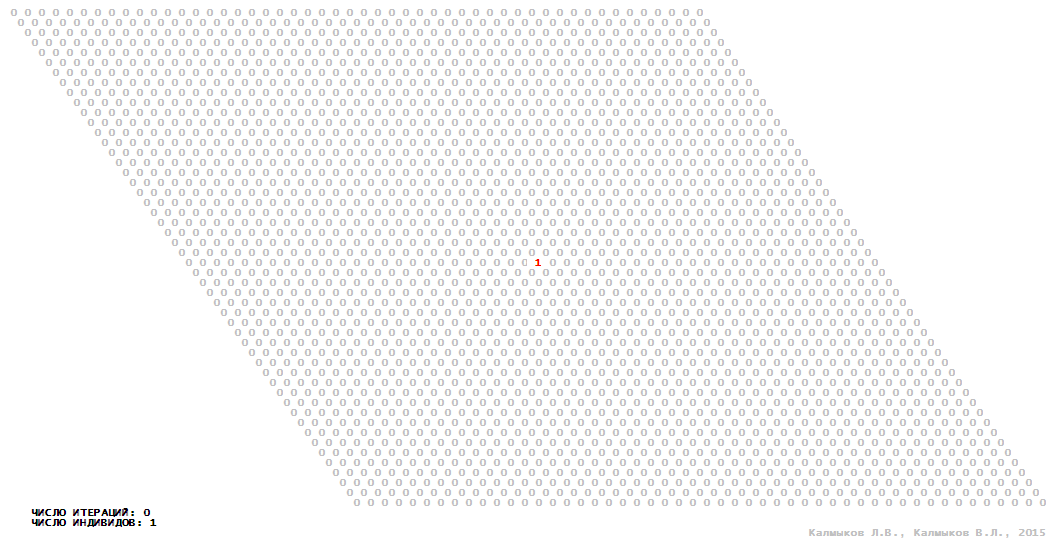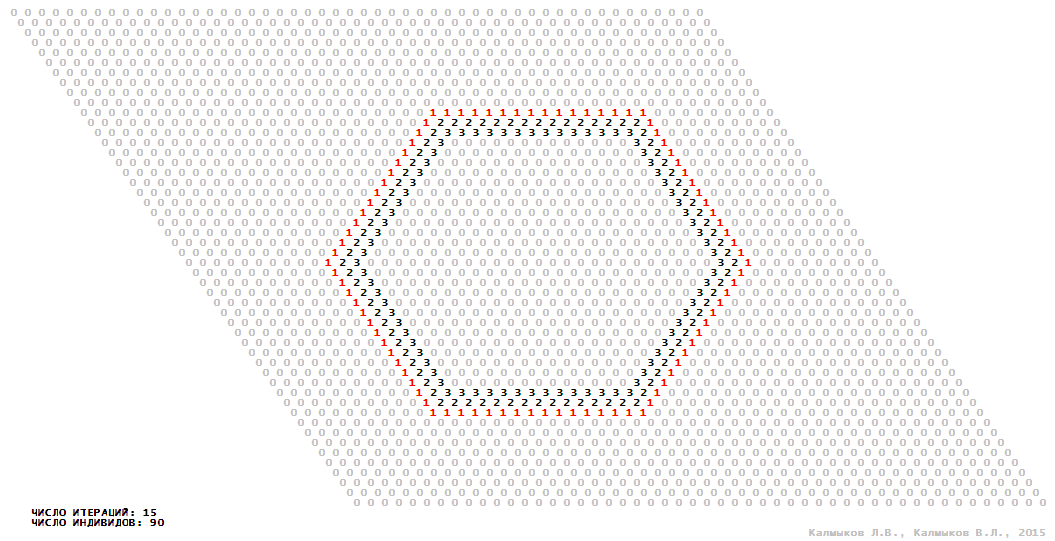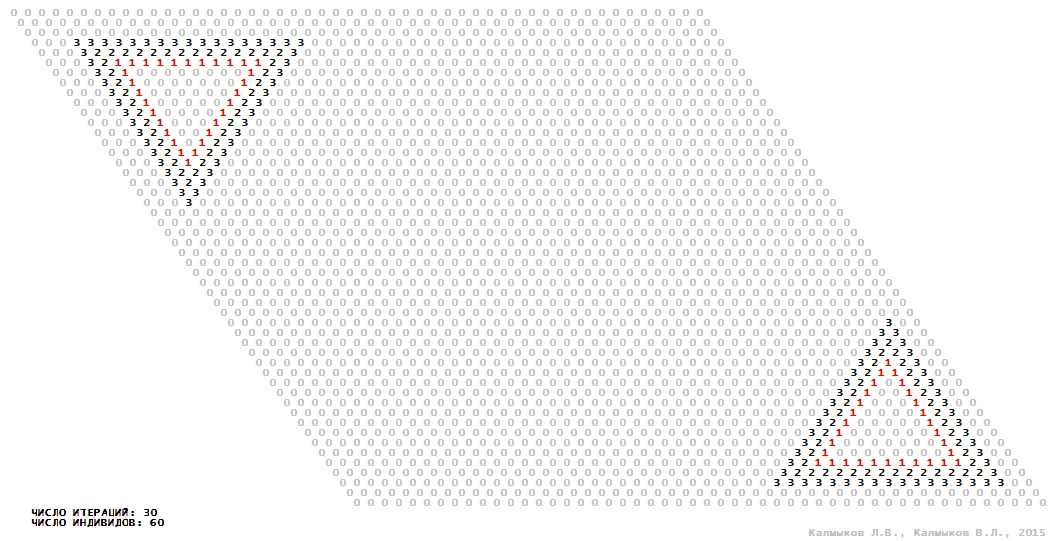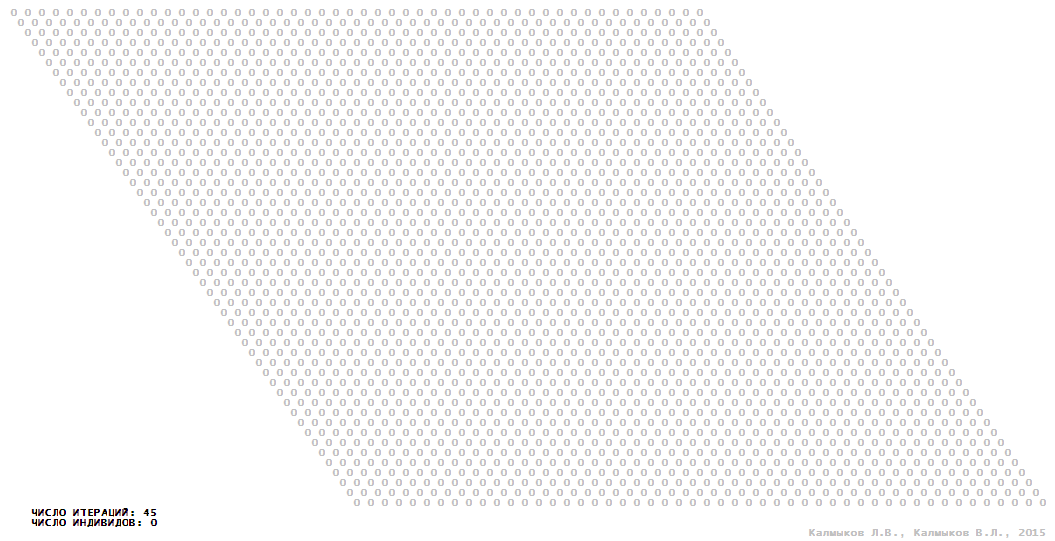

Визуализация 11. Модель 3 с окрестностью фон Неймана.

Визуализация 12. Модель 3 с триподной окрестностью.

Модель 3 — логический детерминированный клеточный автомат с четырьмя состояниями. Множество возможных состояний каждого узла решётки {0, 1, 2, 3}. Решётка клеточного автомата состоит из 50x50 узлов и замкнута периодическими условиями в тор. Длительность восстановления ресурсов занимает две итерации. Используются обозначения: {0} — микроместообитание свободно; {1} — микроместообитание заселено индивидом; {2, 3} — микроместообитание находится в состоянии регенерации, которое длится две итерации. С помощью различных окрестностей исследуется влияние числа потомков и их размещение в пространстве на популяционную динамику. При использовании окрестностей Мура, гексагональной и фон Неймана кривые популяционного роста демонстрируют линейный рост, который резко сменяется падением численности популяции, приводящим к её исчезновению (Рис. 10в), то есть происходили популяционные катастрофы. При использовании триподной окрестности кривая популяционного роста имеет S-образную форму (Рис. 10в), когда происходила успешная колонизация свободного местообитания с дальнейшим неограниченно долгим существованием популяции.

Визуализация 13. Модель 4 с окрестностью Мура.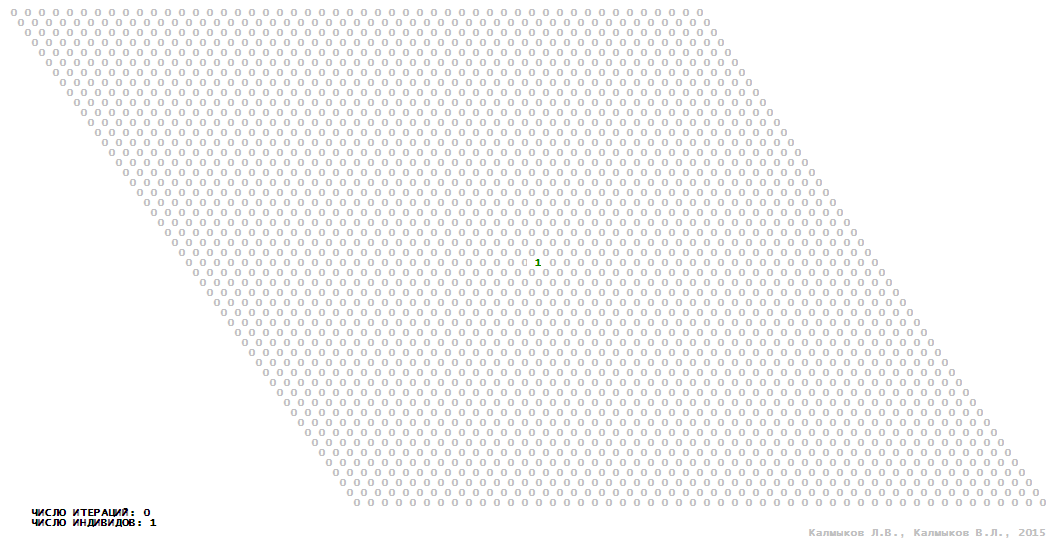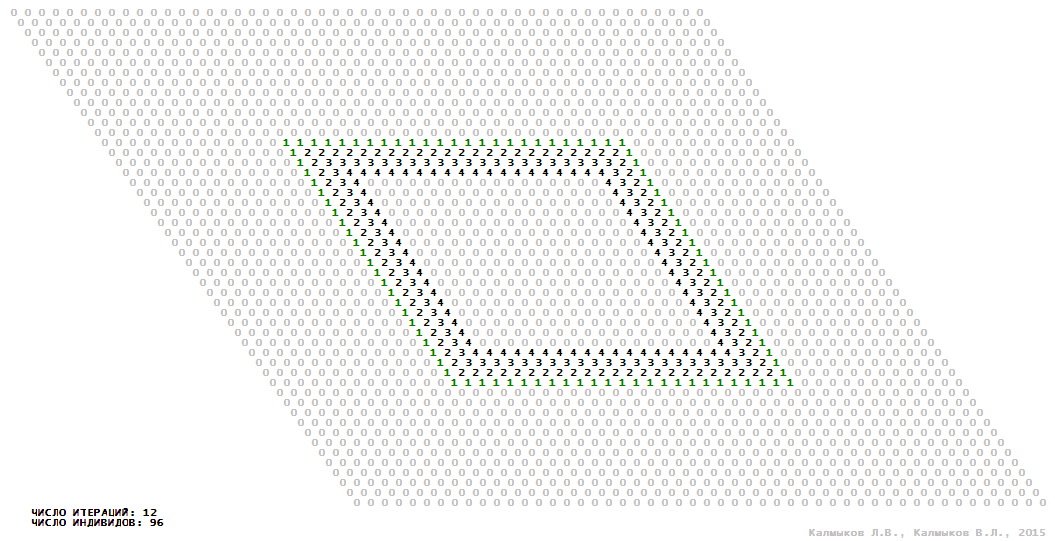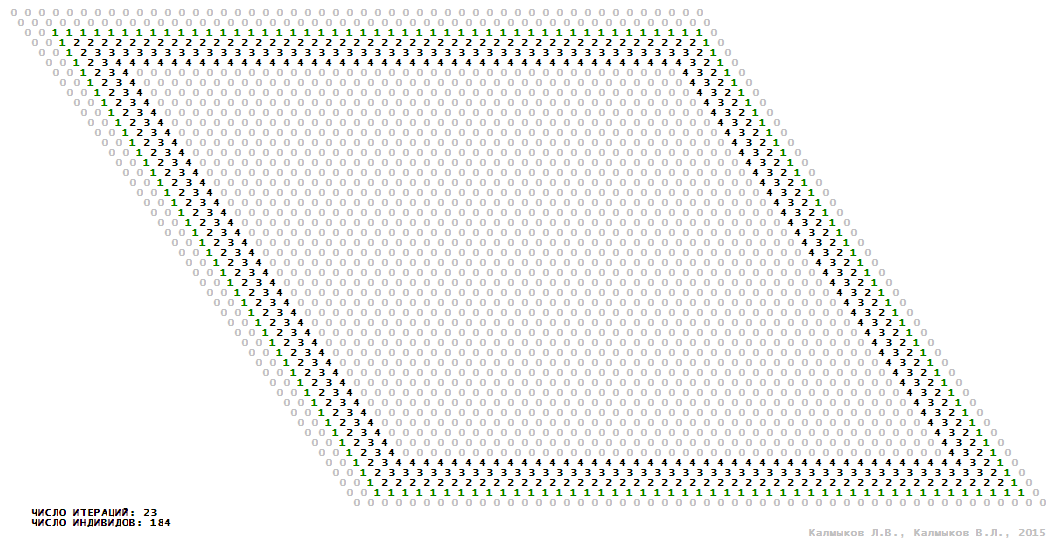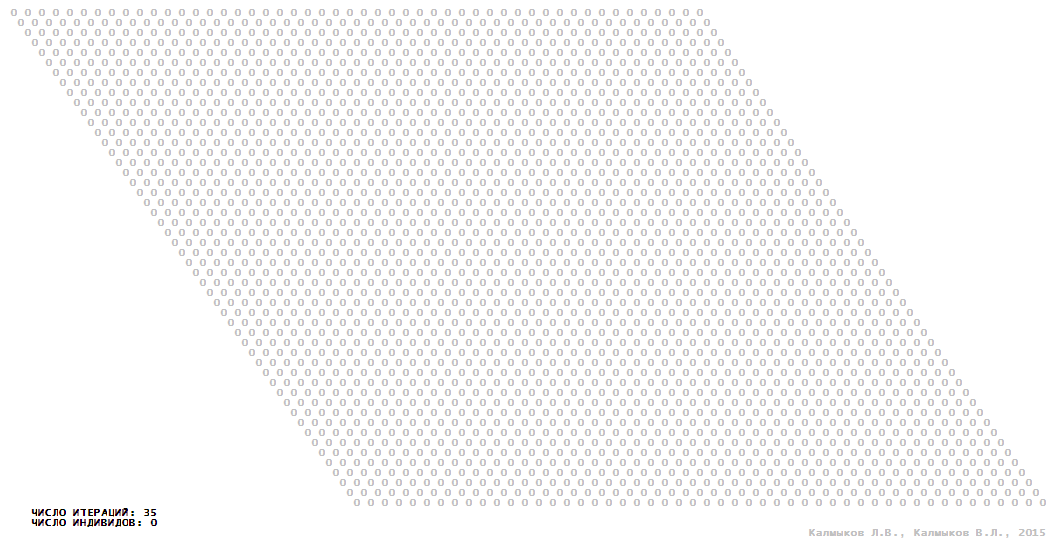

Визуализация 14. Модель 4 с гексагональной окрестностью.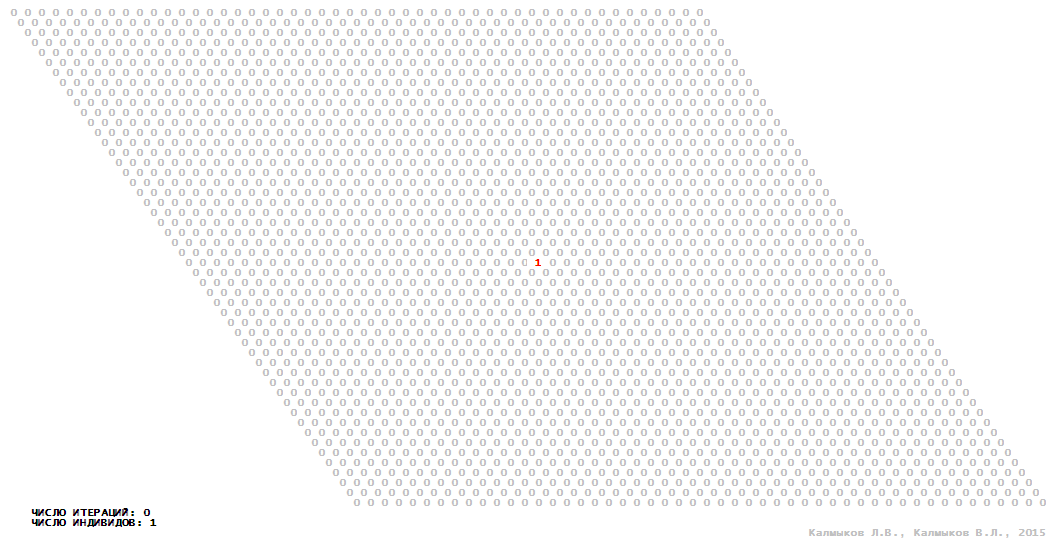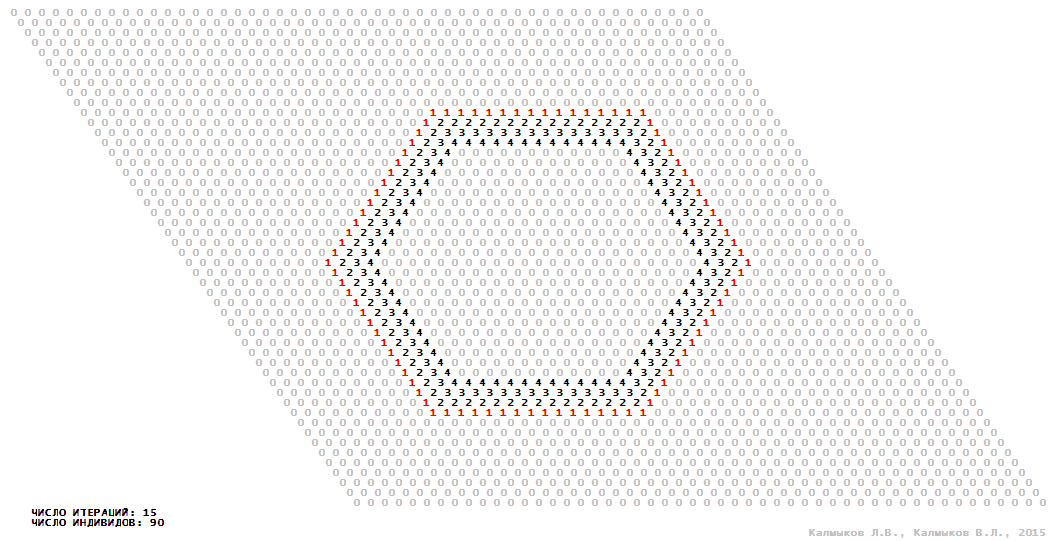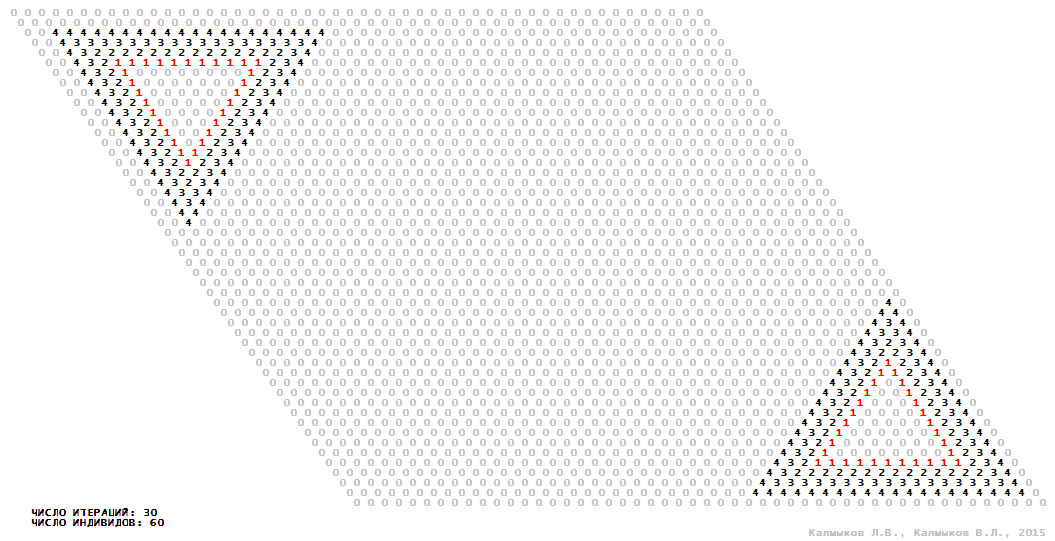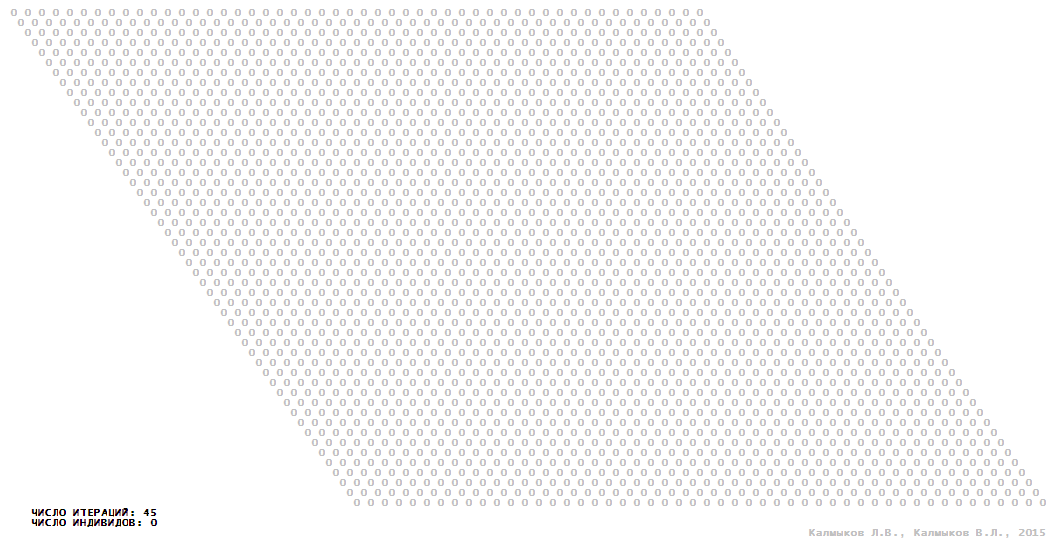

Визуализация 15. Модель 4 с окрестностью фон Неймана.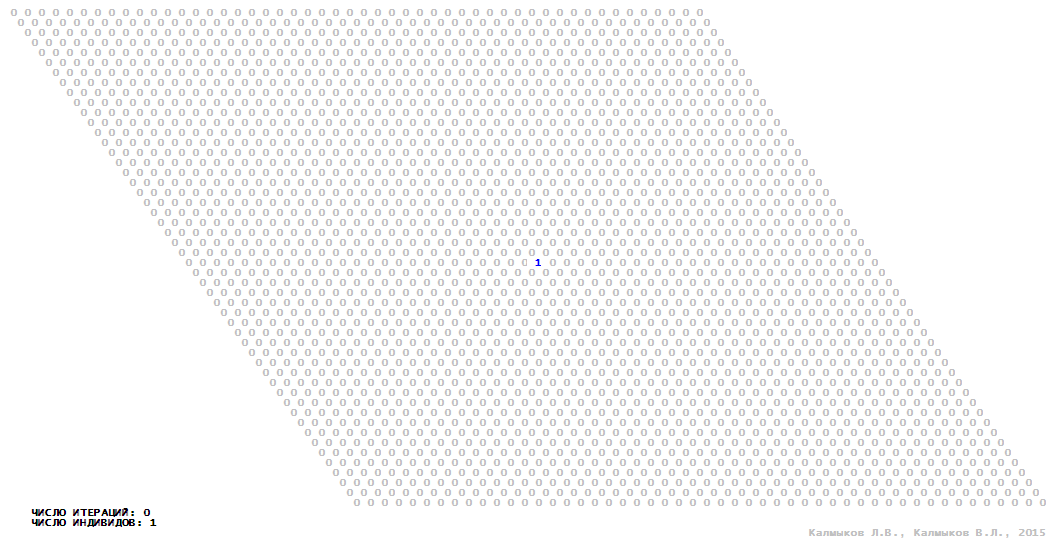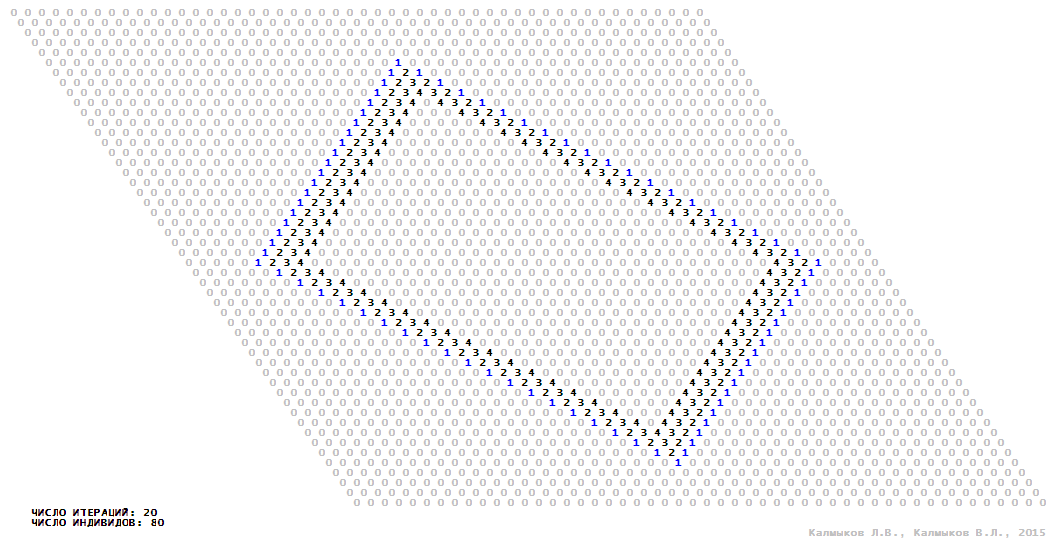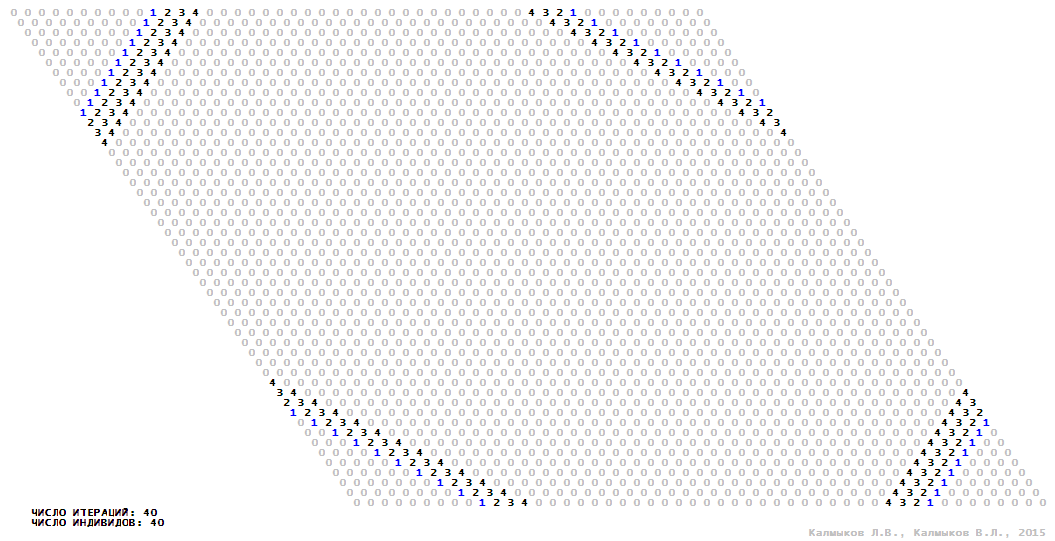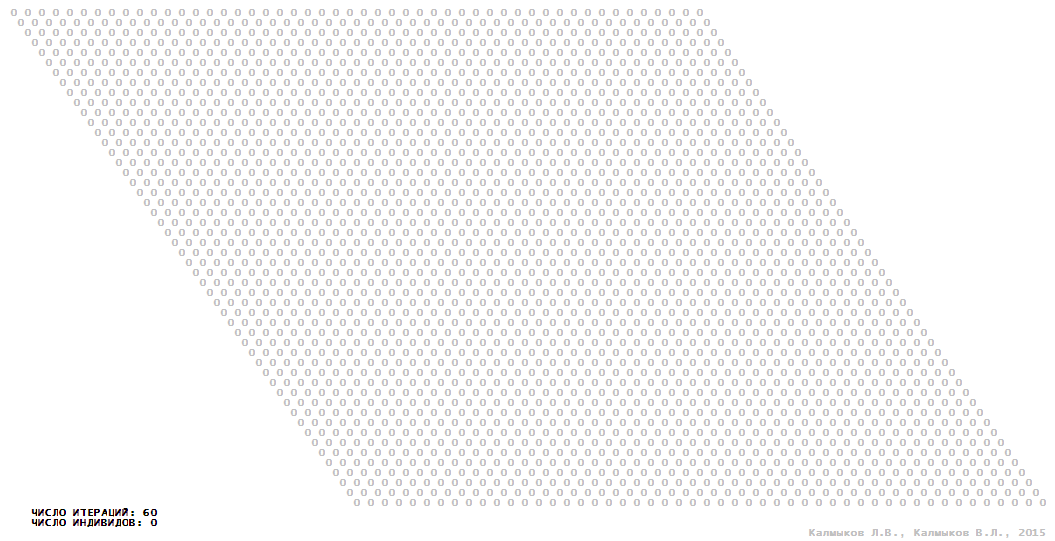

Визуализация 16. Модель 4 с триподной окрестностью.

Модель 4 — логический детерминированный клеточный автомат с пятью состояниями. Множество возможных состояний каждого узла решётки {0, 1, 2, 3, 4}. Решётка клеточного автомата состоит из 50x50 узлов и замкнута периодическими условиями в тор. Длительность восстановления ресурсов занимает три итерации. Используются обозначения: {0} — микроместообитание свободно; {1} — микроместообитание заселено индивидом; {2, 3, 4} — микроместообитание находится в состоянии регенерации, которое длится три итерации. С помощью различных окрестностей исследуется влияние числа потомков и их размещение в пространстве на популяционную динамику. Во всех случаях кривые популяционного роста демонстрируют линейный рост, который резко сменяется падением численности популяции, приводящим к её исчезновению, то есть происходили популяционные катастрофы (Рис. 10г).