Все выпуски
- 2024 Том 16
- 2023 Том 15
- 2022 Том 14
- 2021 Том 13
- 2020 Том 12
- 2019 Том 11
- 2018 Том 10
- 2017 Том 9
- 2016 Том 8
- 2015 Том 7
- 2014 Том 6
- 2013 Том 5
- 2012 Том 4
- 2011 Том 3
- 2010 Том 2
- 2009 Том 1
Математическая модель системы «паразит – хозяин» с распределенным временем сохранения иммунитета
pdf (202K)
Пандемия COVID-19 вызвала рост интереса к математическим моделям эпидемического процесса, так как только статистический анализ заболеваемости не позволяет проводить среднесрочное прогнозирование в условиях быстро меняющейся ситуации.
Среди специфичных особенностей COVID-19, которые нужно учитывать в математических моделях, можно отметить гетерогенность возбудителя, неоднократные смены доминирующего варианта SARS-CoV-2 и относительную кратковременность постинфекционного иммунитета.
В связи с этим были аналитически изучены решения системы дифференциальных уравнений для модели класса SIR с гетерогенной длительностью постинфекционного иммунитета, а также проведены численные расчеты для динамики системы при средней длительности постинфекционного иммунитета порядка года.
Для модели класса SIR с гетерогенной длительностью постинфекционного иммунитета было доказано, что любое решение можно неограниченно продолжать по времени в положительную сторону без выхода за область определения системы.
Для контактного числа $R_0 \leqslant 1$ все решения стремятся к единственномут ривиальному стационарному решению с нулевой долей инфицированных, а для $R_0 > 1$ кроме тривиального решения существует и нетривиальное стационарное решение с ненулевыми долями инфицированных и восприимчивых. Были доказаны существование и единственность нетривиального стационарного решения при $R_0 > 1$, а также доказано, что оно является глобальным аттрактором.
Также для нескольких вариантов гетерогенности были вычислены собственные числа для скорости экспоненциальной сходимости малых отклонений от нетривиального стационарного решения.
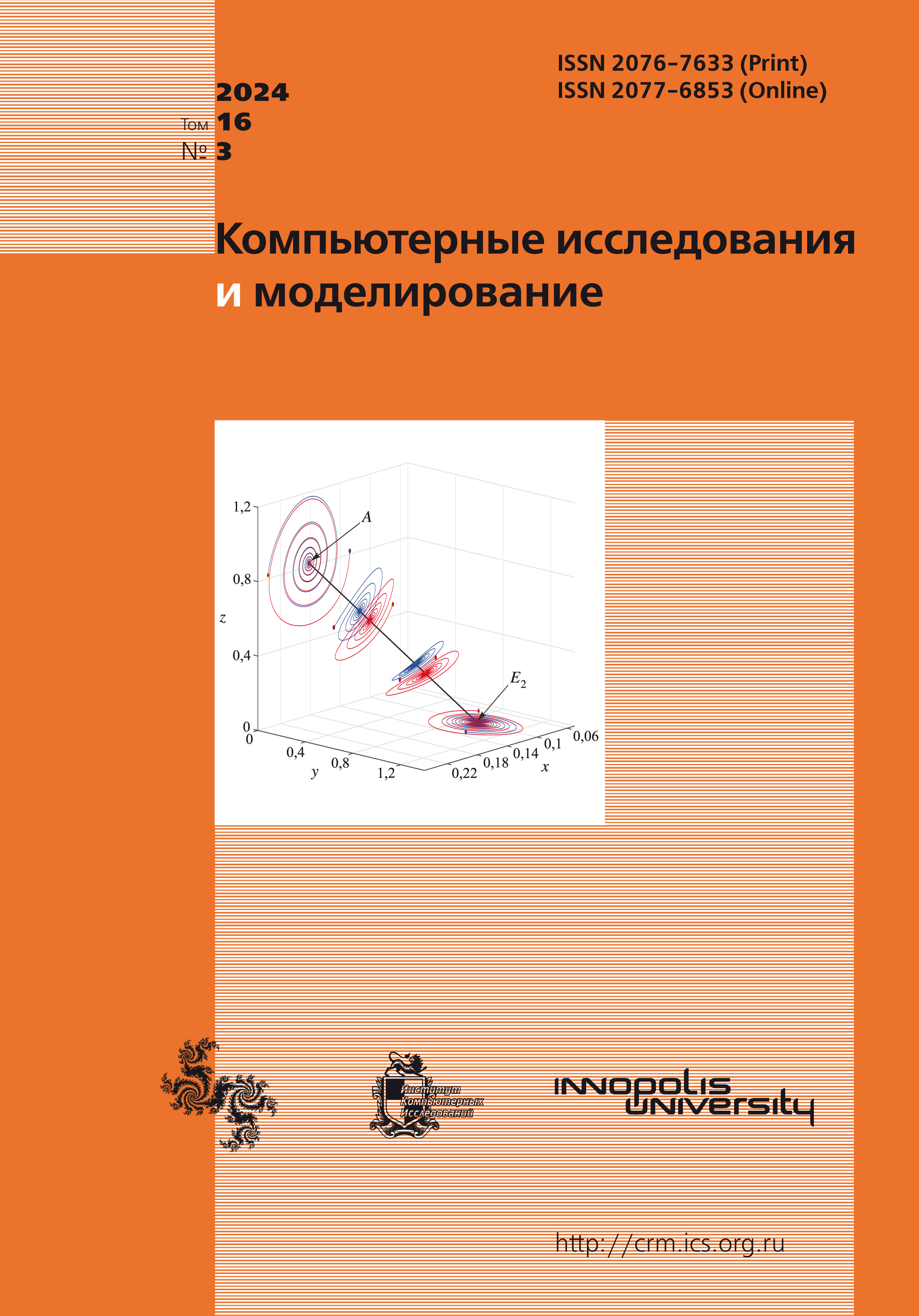
Получено, что при значениях контактного числа, соответствующих COVID-19, фазовая траектория имеет вид скручивающейся спирали с длиной периода порядка года.
Это соответствует реальной динамике заболеваемости COVID-19, при которой после нескольких месяцев роста заболеваемости начинается период его падения. При этом второй волны заболеваемости меньшей амплитуды, что предсказывала модель, не наблюдалось, так как на протяжении 2020–2023 годов примерно каждые полгода появлялся новый вариант SARS-CoV-2, имеющий большую заразность, чем предыдущий, в результате чего новый вариант вытеснял предыдущий и становился доминирующим.
Журнал индексируется в Scopus
Полнотекстовая версия журнала доступна также на сайте научной электронной библиотеки eLIBRARY.RU
Журнал входит в систему Российского индекса научного цитирования.
Журнал включен в базу данных Russian Science Citation Index (RSCI) на платформе Web of Science
Международная Междисциплинарная Конференция "Математика. Компьютер. Образование"
